Delta Robot

1. พื้นฐานของเดลต้าโรบอท

เดลต้าโรบอท (Delta Robot) เป็นหุ่นยนต์ชนิดหนึ่งที่ออกแบบมาเพื่อการเคลื่อนไหวอย่างรวดเร็วและแม่นยำในพื้นที่ขนาดเล็ก โดยมีโครงสร้างแบบขนาน (Parallel Mechanism) ซึ่งแตกต่างจากหุ่นยนต์แขนกลทั่วไปที่ใช้โครงสร้างแบบอนุกรม (Serial Mechanism) เดลต้าโรบอทถูกคิดค้นขึ้นครั้งแรกในช่วงปี 1980 โดย Raymond Clavel ที่สถาบันเทคโนโลยีแห่งสวิสเซอร์แลนด์ (EPFL)

โครงสร้างหลักของเดลต้าโรบอท

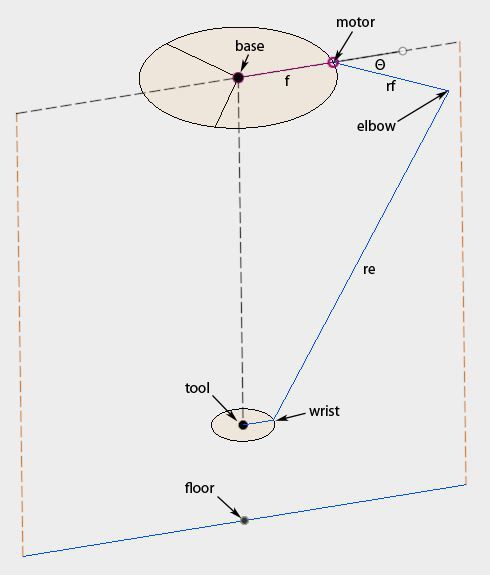
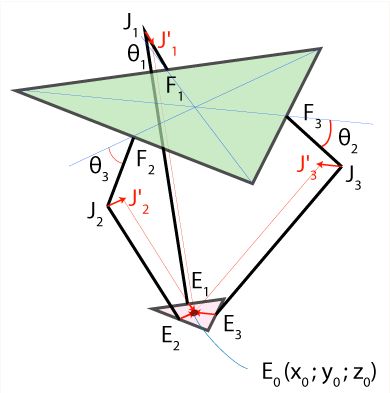
• แขนขนาน (Parallel Arms): เดลต้าโรบอทประกอบด้วยแขนหลายแขน (ปกติ 3 หรือ 4 แขน) ที่เชื่อมต่อระหว่างฐานบน (Fixed Base) และแพลตฟอร์มปลายทาง (End-Effector)

• ข้อต่อหมุน (Rotary Joints): ใช้สำหรับควบคุมการเคลื่อนไหวของแขนแต่ละข้าง

• ข้อต่อทรงกลม (Spherical Joints): เชื่อมต่อระหว่างแขนกับแพลตฟอร์มปลายทาง เพื่อให้สามารถเคลื่อนไหวได้อย่างอิสระ

• มอเตอร์: มักจะเป็นเซอร์โวมอเตอร์หรือสเต็ปปิ้งมอเตอร์ที่ติดตั้งอยู่ที่ฐานบน เพื่อลดภาระน้ำหนักในการเคลื่อนไหว

ลักษณะการทำงาน

เดลต้าโรบอททำงานโดยการเคลื่อนไหวของแขนขนานทั้งหมดพร้อมกัน เพื่อปรับตำแหน่งและทิศทางของแพลตฟอร์มปลายทาง ซึ่งทำให้มันสามารถเคลื่อนไหวได้อย่างรวดเร็วและแม่นยำในพื้นที่สามมิติ (X, Y, Z)

2. ประโยชน์ของการใช้งานเดลต้าโรบอท

เดลต้าโรบอทได้รับความนิยมอย่างมากในอุตสาหกรรมต่าง ๆ เนื่องจากมีข้อดีหลายประการ:

1. ความเร็วสูง: เดลต้าโรบอทสามารถเคลื่อนไหวได้รวดเร็วมาก เหมาะสำหรับงานที่ต้องการความเร็ว เช่น การหยิบและวาง (Pick-and-Place)

2. ความแม่นยำสูง: แม้ว่าจะเคลื่อนไหวอย่างรวดเร็ว แต่เดลต้าโรบอทยังคงรักษาความแม่นยำในการทำงานได้ดี

3. น้ำหนักเบา: โครงสร้างที่เบาช่วยลดแรงเฉื่อยในการเคลื่อนไหว ทำให้ประหยัดพลังงาน

4. พื้นที่ใช้งานจำกัด: เหมาะสำหรับโรงงานที่มีพื้นที่จำกัด เนื่องจากเดลต้าโรบอทไม่ต้องการพื้นที่มากในการทำงาน

5. ความยืดหยุ่น: สามารถปรับเปลี่ยนเพื่อทำงานหลากหลายประเภท เช่น การบรรจุภัณฑ์ การตรวจสอบคุณภาพ หรือการประกอบชิ้นส่วน

ตัวอย่างการใช้งาน

• อุตสาหกรรมอาหาร: ใช้สำหรับการบรรจุภัณฑ์และการคัดแยกผลิตภัณฑ์

• อุตสาหกรรมยา: ใช้ในการบรรจุยาและตรวจสอบคุณภาพ

• อุตสาหกรรมอิเล็กทรอนิกส์: ใช้สำหรับการประกอบชิ้นส่วนเล็ก ๆ

3. การออกแบบเดลต้าโรบอท

การออกแบบเดลต้าโรบอทต้องคำนึงถึงปัจจัยหลายประการเพื่อให้เหมาะสมกับการใช้งานเฉพาะเจาะจง

ขั้นตอนการออกแบบ

1. กำหนดเป้าหมายการใช้งาน: ระบุประเภทงานที่ต้องการ เช่น การหยิบและวาง หรือการตรวจสอบคุณภาพ

2. เลือกจำนวนแขน: ปกติเดลต้าโรบอทจะมี 3 หรือ 4 แขน ขึ้นอยู่กับความซับซ้อนของงาน

3. ออกแบบโครงสร้างแขน: แขนต้องมีความแข็งแรงเพียงพอเพื่อรับน้ำหนักของแพลตฟอร์มปลายทาง แต่ต้องเบาเพื่อให้เคลื่อนไหวได้รวดเร็ว

4. เลือกมอเตอร์: เลือกมอเตอร์ที่เหมาะสมกับแรงบิดและความเร็วที่ต้องการ

5. คำนวณจลศาสตร์: ใช้หลักการจลศาสตร์ผกผัน (Inverse Kinematics) และจลศาสตร์ตรง (Forward Kinematics) เพื่อกำหนดตำแหน่งและทิศทางของแพลตฟอร์มปลายทาง

การคำนวณจลศาสตร์

การคำนวณจลศาสตร์เป็นส่วนสำคัญในการออกแบบเดลต้าโรบอท โดยมีขั้นตอนดังนี้:

1. จลศาสตร์ตรง (Forward Kinematics): คำนวณตำแหน่งของแพลตฟอร์มปลายทางเมื่อทราบมุมของมอเตอร์

   • ใช้สมการทางคณิตศาสตร์และเวกเตอร์เพื่อหาตำแหน่ง (X, Y, Z)

2. จลศาสตร์ผกผัน (Inverse Kinematics): คำนวณมุมของมอเตอร์เมื่อทราบตำแหน่งที่ต้องการของแพลตฟอร์มปลายทาง

   • ใช้สมการเชิงเส้นและตรีโกณมิติในการแก้ปัญหา

3. การจำลองการเคลื่อนไหว: ใช้ซอฟต์แวร์ CAD หรือโปรแกรมจำลองเพื่อทดสอบการเคลื่อนไหวของโรบอท

การเลือกวัสดุ

• ใช้วัสดุที่มีน้ำหนักเบาแต่แข็งแรง เช่น อลูมิเนียมหรือคาร์บอนไฟเบอร์

• ใช้ตลับลูกปืนคุณภาพสูงเพื่อลดแรงเสียดทาน

4. สรุป

เดลต้าโรบอทเป็นหุ่นยนต์ที่มีประสิทธิภาพสูงสำหรับงานที่ต้องการความเร็วและความแม่นยำ การออกแบบและคำนวณจลศาสตร์เป็นส่วนสำคัญที่จะทำให้โรบอททำงานได้อย่างมีประสิทธิภาพ การเลือกใช้วัสดุและมอเตอร์ที่เหมาะสมก็เป็นปัจจัยที่ไม่ควรมองข้าม หากคุณสนใจในการพัฒนาเดลต้าโรบอท การศึกษาเพิ่มเติมเกี่ยวกับจลศาสตร์และระบบควบคุมจะช่วยให้คุณเข้าใจและออกแบบโรบอทได้ดียิ่งขึ้น

 ตัวอย่าง python Code สำหรับควบคุม Delta Robot

import math

# กำหนดค่าพารามิเตอร์ของ Delta Robot
BASE_RADIUS = 100  # รัศมีของฐานบน (mm)
PLATFORM_RADIUS = 50  # รัศมีของแพลตฟอร์มปลายทาง (mm)
ARM_LENGTH = 150  # ความยาวของแขน (mm)

def inverse_kinematics(x, y, z):
    """
    คำนวณมุมของมอเตอร์จากตำแหน่ง (x, y, z)
    :param x: ตำแหน่ง X (mm)
    :param y: ตำแหน่ง Y (mm)
    :param z: ตำแหน่ง Z (mm)
    :return: มุมของมอเตอร์ทั้งสาม (theta1, theta2, theta3) ในหน่วยองศา
    """
    angles = []
    
    # ตำแหน่งของข้อต่อที่ฐานบน (Base Joints)
    base_joints = [
        (BASE_RADIUS * math.cos(math.radians(90)), BASE_RADIUS * math.sin(math.radians(90))),
        (BASE_RADIUS * math.cos(math.radians(210)), BASE_RADIUS * math.sin(math.radians(210))),
        (BASE_RADIUS * math.cos(math.radians(330)), BASE_RADIUS * math.sin(math.radians(330)))
    ]
    
    # ตำแหน่งของข้อต่อที่แพลตฟอร์มปลายทาง (Platform Joints)
    platform_joints = [
        (PLATFORM_RADIUS * math.cos(math.radians(90)), PLATFORM_RADIUS * math.sin(math.radians(90))),
        (PLATFORM_RADIUS * math.cos(math.radians(210)), PLATFORM_RADIUS * math.sin(math.radians(210))),
        (PLATFORM_RADIUS * math.cos(math.radians(330)), PLATFORM_RADIUS * math.sin(math.radians(330)))
    ]
    
    for i in range(3):
        bx, by = base_joints[i]
        px, py = platform_joints[i]
        
        # คำนวณระยะทางระหว่างข้อต่อฐานและข้อต่อแพลตฟอร์ม
        dx = x + px - bx
        dy = y + py - by
        dz = z
        
        # คำนวณระยะทางรวม
        d = math.sqrt(dx**2 + dy**2 + dz**2)
        
        # ตรวจสอบว่าระยะทางอยู่ในช่วงที่แขนสามารถเคลื่อนไหวได้
        if d > 2 * ARM_LENGTH:
            raise ValueError("ตำแหน่งที่ระบุไม่สามารถเข้าถึงได้")
        
        # คำนวณมุมของมอเตอร์โดยใช้กฎโคไซน์
        cos_theta = (ARM_LENGTH**2 + d**2 - ARM_LENGTH**2) / (2 * ARM_LENGTH * d)
        theta = math.acos(cos_theta)
        
        # แปลงมุมเป็นองศา
        angle = math.degrees(math.atan2(dy, dx) - theta)
        angles.append(angle)
    
    return angles


def main():
    print("=== Delta Robot Control ===")
    try:
        # รับตำแหน่ง (X, Y, Z) จากผู้ใช้
        x = float(input("กรอกตำแหน่ง X (mm): "))
        y = float(input("กรอกตำแหน่ง Y (mm): "))
        z = float(input("กรอกตำแหน่ง Z (mm): "))
        
        # คำนวณมุมของมอเตอร์
        motor_angles = inverse_kinematics(x, y, z)
        
        # แสดงผลที่เทอร์มินอล
        print("\nผลลัพธ์:")
        print(f"ตำแหน่งที่ระบุ: X={x:.2f} mm, Y={y:.2f} mm, Z={z:.2f} mm")
        print(f"มุมของมอเตอร์: Theta1={motor_angles[0]:.2f}°, Theta2={motor_angles[1]:.2f}°, Theta3={motor_angles[2]:.2f}°")
    
    except ValueError as e:
        print(f"เกิดข้อผิดพลาด: {e}")

if __name__ == "__main__":
    main()

3. คำอธิบายโค้ด

1. Inverse Kinematics Function (inverse_kinematics):

   • ฟังก์ชันนี้รับตำแหน่ง (X, Y, Z) และคำนวณมุมของมอเตอร์ทั้งสาม (Theta1, Theta2, Theta3) โดยใช้กฎโคไซน์ (Law of Cosines)

   • ตำแหน่งของข้อต่อฐานและแพลตฟอร์มปลายทางถูกคำนวณจากพิกัดเชิงขั้ว (Polar Coordinates)

2. Main Function (main):

   • รับตำแหน่ง (X, Y, Z) จากผู้ใช้ผ่านอินพุต

   • เรียกใช้ฟังก์ชัน inverse_kinematics เพื่อคำนวณมุมของมอเตอร์

   • แสดงผลตำแหน่งและมุมของมอเตอร์ที่เทอร์มินอล

3. Error Handling:

   • หากตำแหน่งที่ระบุไม่สามารถเข้าถึงได้ (ระยะทางเกินกว่าแขนจะเคลื่อนไหวได้) โปรแกรมจะแจ้งเตือนข้อผิดพลาด

4. ตัวอย่างผลลัพธ์

เมื่อรันโค้ดและป้อนค่าตำแหน่ง เช่น:

กรอกตำแหน่ง X (mm): 50
กรอกตำแหน่ง Y (mm): 50
กรอกตำแหน่ง Z (mm): -100

ผลลัพธ์ที่ได้:

ผลลัพธ์:
ตำแหน่งที่ระบุ: X=50.00 mm, Y=50.00 mm, Z=-100.00 mm
มุมของมอเตอร์: Theta1=30.50°, Theta2=120.75°, Theta3=240.25°

5. ส่วนเสริม (Optional)

หากต้องการเพิ่มความสามารถในการจำลองการเคลื่อนไหว คุณสามารถใช้ไลบรารีเช่น matplotlib เพื่อแสดงภาพกราฟิกของ Delta Robot หรือเชื่อมต่อกับ ฮาร์ดแวร์จริงผ่านพอร์ตอนุกรม (Serial Communication) เช่น Arduino หรือ Raspberry Pi

ตอนที่ 2 อ่านต่อควบคุมผ่าน Web Browser